STA 235H - Natural Experiments & Difference-In-Differences
Fall 2023
McCombs School of Business, UT Austin
Announcements
Grades for Homework 2 will be posted this week.
Review the Answer Key on the course website (posted Mon/Tue after submission).
Everyone did pretty well, but remember that answers need to match submitted code.
Announcements
Grades for Homework 2 will be posted this week.
Review the Answer Key on the course website (posted Mon/Tue after submission).
Everyone did pretty well, but remember that answers need to match submitted code.
Midterm is in class (week of Oct. 16th):
Practice quizz (not graded, but mandatory) for proctored exams (HonorLock).
There will be a review session Thur/Fri before the midterm (poll).
Last week

Finished with randomized controlled trials.
- Limitations in generalizability and interference (e.g. spillovers).
Introduced observational studies:
- Controlling for observable confounders (e.g. regression and matching)
Today
Talk about other Observational Studies:
Natural Experiments
Difference-in-Differences
First half: Material
Second half: You will tackle an exercise.

Recap so far
What did we see last week?
- Limitations in RCTs:
What did we see last week?
Limitations in RCTs:
Generalizability
Breaking SUTVA: Spillover effects and General Equilibrium Effects.
What did we see last week?
Limitations in RCTs:
Generalizability
Breaking SUTVA: Spillover effects and General Equilibrium Effects.
Introduced Observational Studies:
We need to control by confouders: Conditional Ignorability Assumption.
How? E.g. Regression, Matching.
Identification strategies (designs) we have seen so far...
Randomized Controlled trials (RCTs)
Identification strategies (designs) we have seen so far...
Randomized Controlled trials (RCTs)
Treatment assignment is randomized
Ignorability assumption holds by design: Groups are comparable in obs. and unobs. characteristics.
Identification strategies (designs) we have seen so far...
Randomized Controlled trials (RCTs)
Treatment assignment is randomized
Ignorability assumption holds by design: Groups are comparable in obs. and unobs. characteristics.
Analysis? (i) Check balance and (ii) difference in means.
Identification strategies (designs) we have seen so far...
Selection on Observables (Matching, Regressions with covariates):
Identification strategies (designs) we have seen so far...
Selection on Observables (Matching, Regressions with covariates):
Treatment assignment is not randomized
Conditional independence assumption holds if we can control for all confounders (assumes all confounders are observed)
- After adjusting for covariates, assignment to treatment is as good as random (Is this a credible assumption?).
Identification strategies (designs) we have seen so far...
Selection on Observables (Matching, Regressions with covariates):
Treatment assignment is not randomized
Conditional independence assumption holds if we can control for all confounders (assumes all confounders are observed)
- After adjusting for covariates, assignment to treatment is as good as random (Is this a credible assumption?).
Analysis? (i) Compare balance before matching, (ii) compare balance after matching, and (iii) difference in means for the matched sample.
Is there randomness out there?
Finding "RCTs" in the wild
- Given that we can't run RCTs for everything, the next best thing is finding a source of random variation that, for all practical purposes, would work as an RCT
Finding "RCTs" in the wild
- Given that we can't run RCTs for everything, the next best thing is finding a source of random variation that, for all practical purposes, would work as an RCT
Natural Experiments
You, as a researcher, did not assign units to treatment levels
Finding "RCTs" in the wild
- Given that we can't run RCTs for everything, the next best thing is finding a source of random variation that, for all practical purposes, would work as an RCT
Natural Experiments
You, as a researcher, did not assign units to treatment levels
Random: Assignment to an intervention is random (e.g. lottery)
As if random: Assignment to an intervention is not random, but it's not correlated with potential outcomes.
Finding "RCTs" in the wild
- Given that we can't run RCTs for everything, the next best thing is finding a source of random variation that, for all practical purposes, would work as an RCT
Natural Experiments
You, as a researcher, did not assign units to treatment levels
Random: Assignment to an intervention is random (e.g. lottery)
As if random: Assignment to an intervention is not random, but it's not correlated with potential outcomes.
Context matters!
Examples of natural experiments
- Oregon Health experiment: Lotteries for Medicaid expansion.
Examples of natural experiments
Oregon Health experiment: Lotteries for Medicaid expansion.
Vietnam Draft: Impact of military service/education (GI Bill) on earnings.
Examples of natural experiments
Oregon Health experiment: Lotteries for Medicaid expansion.
Vietnam Draft: Impact of military service/education (GI Bill) on earnings.
Lottery winners: Impact of unearned income on labor earnings.
Examples of natural experiments
Oregon Health experiment: Lotteries for Medicaid expansion.
Vietnam Draft: Impact of military service/education (GI Bill) on earnings.
Lottery winners: Impact of unearned income on labor earnings.
We can analyze these cases just like an RCT
Examples of natural experiments
Oregon Health experiment: Lotteries for Medicaid expansion.
Vietnam Draft: Impact of military service/education (GI Bill) on earnings.
Lottery winners: Impact of unearned income on labor earnings.
We can analyze these cases just like an RCT
What do we do if we have something like a natural experiment but both our groups are not necessarily balanced?
Two wrongs make a right
Raising the minimum wage
What happens if we raise the minimum wage
Raising the minimum wage
What happens if we raise the minimum wage
Economic theory says there should be fewer jobs
Raising the minimum wage
What happens if we raise the minimum wage
Economic theory says there should be fewer jobs
New Jersey in 1992
$4.25 → $5.05
The setup
Before vs After
Avg. # of jobs per fast food restaurant in NJ
Before vs After
Avg. # of jobs per fast food restaurant in NJ
New Jerseybefore = 20.44
Before vs After
Avg. # of jobs per fast food restaurant in NJ
New Jerseybefore = 20.44
New Jerseyafter = 21.03
Before vs After
Avg. # of jobs per fast food restaurant in NJ
New Jerseybefore = 20.44
New Jerseyafter = 21.03
∆ = 0.59
Before vs After
Avg. # of jobs per fast food restaurant in NJ
New Jerseybefore = 20.44
New Jerseyafter = 21.03
∆ = 0.59
Is this a causal effect?
Treatment vs Control
Avg. # of jobs per fast food restaurant
Treatment vs Control
Avg. # of jobs per fast food restaurant
Pennsylvaniaafter = 21.17
Treatment vs Control
Avg. # of jobs per fast food restaurant
Pennsylvaniaafter = 21.17
New Jerseyafter = 21.03
Treatment vs Control
Avg. # of jobs per fast food restaurant
Pennsylvaniaafter = 21.17
New Jerseyafter = 21.03
∆ = -0.14
Treatment vs Control
Avg. # of jobs per fast food restaurant
Pennsylvaniaafter = 21.17
New Jerseyafter = 21.03
∆ = -0.14
Is this a causal effect?
Problems
Before vs After
Only looking at the treatment group
Impossible to separate changes because of treatment or time
Problems
Before vs After
Only looking at the treatment group
Impossible to separate changes because of treatment or time
Treatment vs Control
Only looking at post-treatment values
Impossible to separate changes because of treatment or differences in growth/other confounders

Difference-in-Differences
The idea of a DD analysis is to take the within-unit growth...
| Pre mean | Post mean | ∆ (post − pre) | |
|---|---|---|---|
| Control | A (never treated) |
B (never treated) |
B − A |
| Treatment | C (not yet treated) |
D (treated) |
D − C |
| ∆ (treatment − control) |
A − C | B − D | (B − A) − (D − C) or (B − D) − (A − C) |
∆ (post − pre) = within-unit growth
Difference-in-Differences
... and the across-group growth...
| Pre mean | Post mean | ∆ (post − pre) | |
|---|---|---|---|
| Control | A (never treated) |
B (never treated) |
B − A |
| Treatment | C (not yet treated) |
D (treated) |
D − C |
| ∆ (treatment − control) |
C − A | D − B | (B − A) − (D − C) or (B − D) − (A − C) |
∆ (treatment − control) = across-group growth
Difference-in-Differences
... and combine them!
| Pre mean | Post mean | ∆ (post − pre) | |
|---|---|---|---|
| Control | A (never treated) |
B (never treated) |
B − A |
| Treatment | C (not yet treated) |
D (treated) |
D − C |
| ∆ (treatment − control) |
C − A | D − B | (D − C) − (B − A) or (D − B) − (C − A) |
∆within units − ∆across groups =
Difference-in-differences =
causal effect!
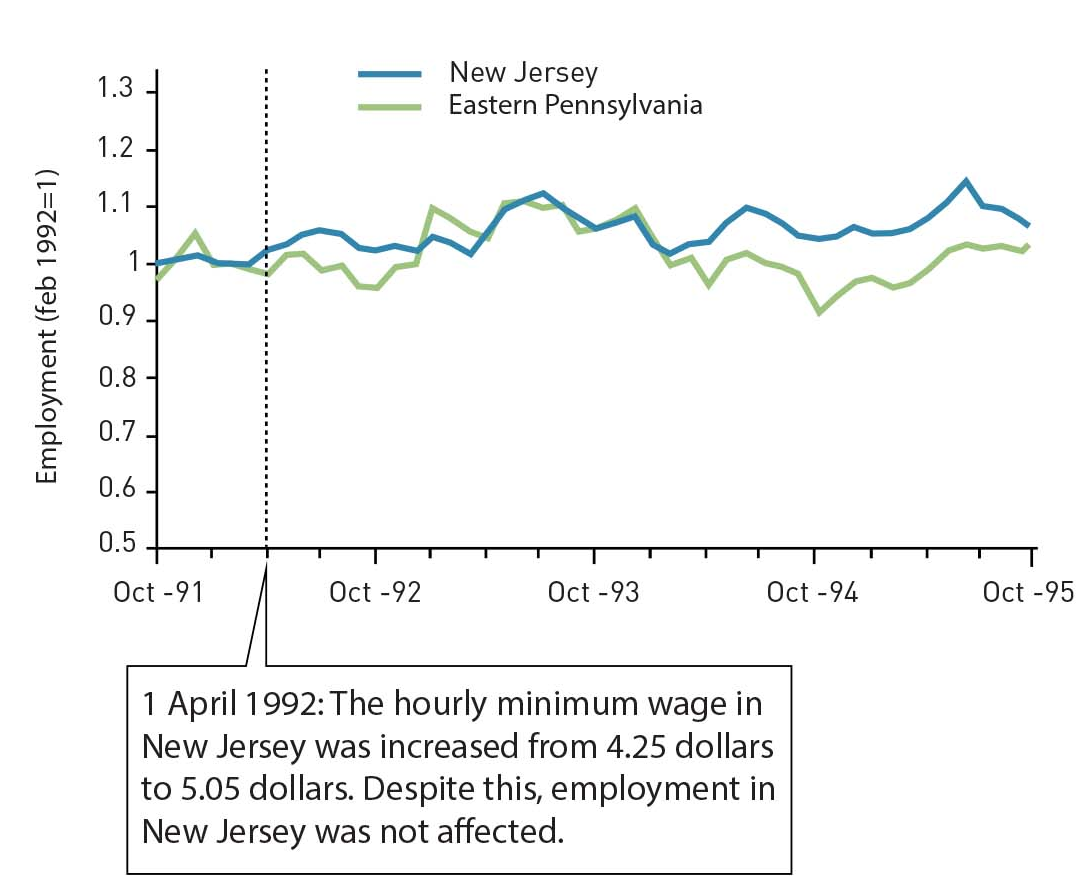
Coming back to New Jersey
| Pre mean | Post mean | ∆ (post − pre) | |
|---|---|---|---|
| Pennsylvania | 23.33 A |
21.17 B |
-2.16 B − A |
| New Jersey | 20.44 C |
21.03 D |
0.59 D − C |
| ∆ (NJ − PA) |
-2.89 C − A |
-0.14 D − B |
(0.59) − (−2.16) = 2.76 |
How does it look in a plot?
... And the real plot!
Difference-in-Differences in practice
- There's no need to manually estimate all group means..
Difference-in-Differences in practice
- There's no need to manually estimate all group means..
We can use regressions!
Difference-in-Differences in practice
- There's no need to manually estimate all group means..
We can use regressions!
- If the two dimensions for our DD are time and treatment:
Yi=β0+β1Treati+β2Posti+β3Treati×Posti+εi where Treat=1 for the treatment group, and Post=1 for the after period.
Difference-in-Differences in practice
- There's no need to manually estimate all group means..
We can use regressions!
- If the two dimensions for our DD are time and treatment:
Yi=β0+β1Treati+β2Posti+β3Treati×Posti+εi where Treat=1 for the treatment group, and Post=1 for the after period.
Can you identify the different coefficients?
Difference-in-Differences in practice
- There's no need to manually estimate all group means..
We can use regressions!
- If the two dimensions for our DD are time and treatment:
Yi=β0+β1Treati+β2Posti+β3Treati×Posti+εi where Treat=1 for the treatment group, and Post=1 for the after period.
β3 is the causal effect!
Let's see it with data
minwage <- read.csv("https://raw.githubusercontent.com/maibennett/sta235/main/exampleSite/content/Classes/Week7/1_DiffInDiff/data/minwage.csv")minwage <- minwage %>% mutate(treat = ifelse(location=="PA", 0, 1), # treat group: the treated state post = ifelse(date=="nov1992", 1, 0)) # post: time after treatment was set in placehead(minwage)## chain location wage full part date treat post## 1 wendys PA 5.00 20 20 feb1992 0 0## 2 wendys PA 5.50 6 26 feb1992 0 0## 3 burgerking PA 5.00 50 35 feb1992 0 0## 4 burgerking PA 5.00 10 17 feb1992 0 0## 5 kfc PA 5.25 2 8 feb1992 0 0## 6 kfc PA 5.00 2 10 feb1992 0 0Let's see it with data
summary(lm(full ~ treat*post, data = minwage))## ## Call:## lm(formula = full ~ treat * post, data = minwage)## ## Residuals:## Min 1Q Median 3Q Max ## -10.664 -5.971 -2.405 3.653 52.029 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 10.664 1.007 10.589 <2e-16 ***## treat -2.693 1.117 -2.411 0.0162 * ## post -2.493 1.424 -1.750 0.0805 . ## treat:post 2.927 1.580 1.853 0.0643 . ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 8.243 on 712 degrees of freedom## Multiple R-squared: 0.008207, Adjusted R-squared: 0.004028 ## F-statistic: 1.964 on 3 and 712 DF, p-value: 0.118- Can you interpret the treatment effect?
Let's see it with data
summary(lm(full ~ treat*post, data = minwage))## ## Call:## lm(formula = full ~ treat * post, data = minwage)## ## Residuals:## Min 1Q Median 3Q Max ## -10.664 -5.971 -2.405 3.653 52.029 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 10.664 1.007 10.589 <2e-16 ***## treat -2.693 1.117 -2.411 0.0162 * ## post -2.493 1.424 -1.750 0.0805 . ## treat:post 2.927 1.580 1.853 0.0643 . ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 8.243 on 712 degrees of freedom## Multiple R-squared: 0.008207, Adjusted R-squared: 0.004028 ## F-statistic: 1.964 on 3 and 712 DF, p-value: 0.118- Can you interpret the treatment effect?
"Increasing the minimum wage from $4.25 to $5.05 had an average effect in New Jersey of 2.9 additional jobs per fast food restaurant"
Important things to note
In Difference-in-Differences, groups do not need to be balanced
- If differences are stable over time, they get cancelled out when doing the Diff-in-Diff.
Important things to note
In Difference-in-Differences, groups do not need to be balanced
- If differences are stable over time, they get cancelled out when doing the Diff-in-Diff.
Difference-in-Differences provides an estimate for an average treatment effect for the treated group
- The estimated effect is not generalizable for the entire sample, only for the treated group.
Diff-in-Diff Assumptions
Assumptions
Parallel Trends
Assumptions
Parallel Trends
In the absence of the intervention, treatment and control group would have changed in the same way
If parallel trends assumption hold...
If parallel trends assumption doesn't hold...
... the DD estimate will be biased
Robustness Check
Pre-Parallel Trends
Robustness Check
Pre-Parallel Trends
Check by pretending the treatment happened earlier; if there's an effect, there's likely an underlying trend
Use the pre-intervention period and conduct a placebo DD
Your turn
Wrapping up
We introduced a new study design!
If we think the parallel trend assumption holds, we can find an Average Treatment Effect for the treated group (ATT)
- Remember that we can't say anything about the treatment effect for the control group!
Next week we will see more identification strategies.

References
Angrist, J. and S. Pischke. (2015). "Mastering Metrics". Chapter 2.
Angrist, J. and S. Pischke. (2015). "Mastering Metrics". Chapter 5.
Heiss, A. (2020). "Program Evaluation for Public Policy". Class 8-9: Diff-in-diff I and II, Course at BYU.