+ - 0:00:00
Notes for current slide
Notes for next slide

STA 235H - RCTs and Observational Studies

Fall 2023

McCombs School of Business, UT Austin

1 / 31

Housekeeping

  • Let's talk about ChatGPT.

    • Should be use as a complement of learning, not a substitute.

    • ChatGPT is mainly useful when you are able to check the accuracy of its answers.

    • You need to do your own work.

2 / 31

Housekeeping

  • Let's talk about ChatGPT.

    • Should be use as a complement of learning, not a substitute.

    • ChatGPT is mainly useful when you are able to check the accuracy of its answers.

    • You need to do your own work.

  • No Office Hours this Thursday.

    • I will hold OH (for this week) on Tues (4pm - 5:30pm) and Wed (10:30am - 11:30am)
2 / 31

Last week

  • We talked about the Ignorability Assumption

  • Started discussing randomized controlled trials.

    • Why they are the gold standard.

    • How to analyze them.

3 / 31

Today

  • Discuss about limitations of RCTs:

    • Generalizability
    • Spillover/General equilibrium effects.

  • What is selection on observables?:

    • Omitted Variable Bias

    • Regression Adjustment

    • Matching

4 / 31

Limitations of RCTs

5 / 31

Recap

  • RCTs make the ignorability assumption hold by design
6 / 31

Recap

  • RCTs make the ignorability assumption hold by design

How?

6 / 31

Recap

  • RCTs make the ignorability assumption hold by design

How?

6 / 31

Examples of RCTs

7 / 31

Examples of RCTs

7 / 31

Steps to analyze a RCT?

8 / 31

Steps to analyze a RCT?

1) Check for balance

(Remember to transform categorical variables into binary ones!)

8 / 31

Steps to analyze a RCT?

1) Check for balance

(Remember to transform categorical variables into binary ones!)

2) Estimate diff.
in means

(Simple regression
between Y and Z)

8 / 31

Steps to analyze a RCT?

1) Check for balance

(Remember to transform categorical variables into binary ones!)

2) Estimate diff.
in means

(Simple regression
between Y and Z)

2)* Estimate diff. in means with covariates

(Multiple regression between Y and Z, adding other baseline covariates X)

8 / 31

Potential issues to have in mind

9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

  • Where did we get our sample for our study from? Is it representative of a larger population?
9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

  • Where did we get our sample for our study from? Is it representative of a larger population?

Spillover effects

9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

  • Where did we get our sample for our study from? Is it representative of a larger population?

Spillover effects

  • Can an individual in the control group be affected by the treatment?
9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

  • Where did we get our sample for our study from? Is it representative of a larger population?

Spillover effects

  • Can an individual in the control group be affected by the treatment?

General equilibrium effects

9 / 31

Potential issues to have in mind

Generalizability of our estimated effects (External Validity)

  • Where did we get our sample for our study from? Is it representative of a larger population?

Spillover effects

  • Can an individual in the control group be affected by the treatment?

General equilibrium effects

  • What happens if we scale up an intervention? Will the effect be the same?
9 / 31

External vs Internal Validity

10 / 31

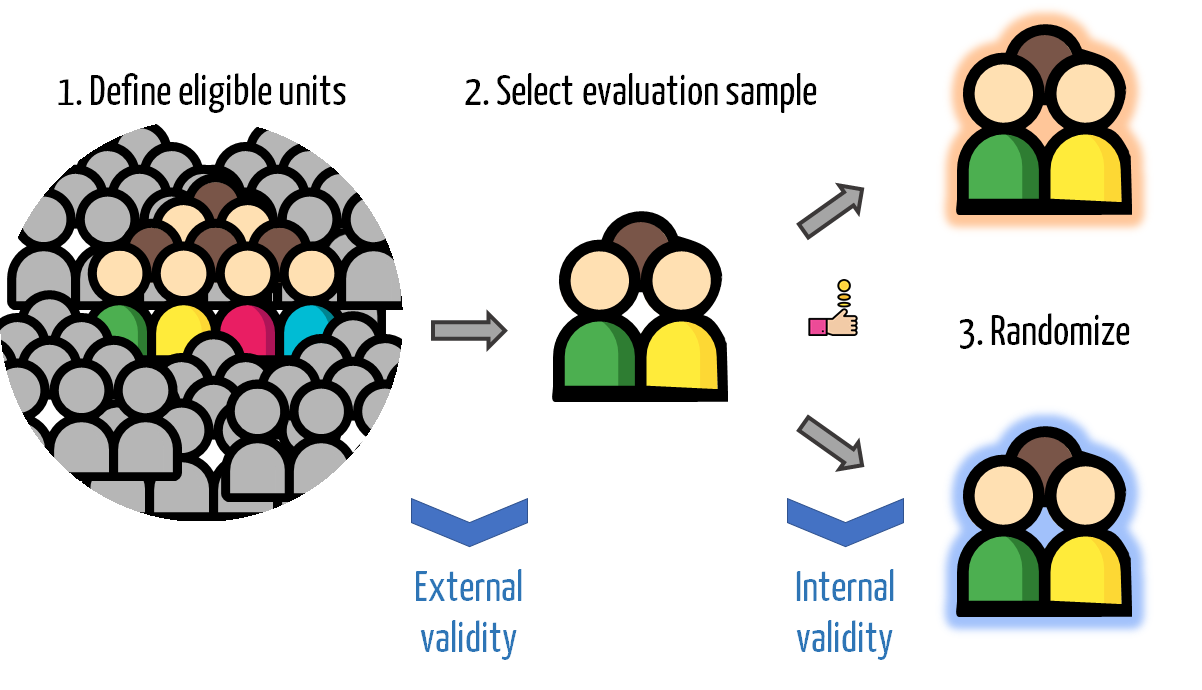
External vs Internal Validity

  • Many times, RCTs use convenience samples
10 / 31

SUTVA: No interference

  • Aside from ignorability, RCTs rely on the Stable Unit Treatment Value Assumption (SUTVA)
11 / 31

SUTVA: No interference

  • Aside from ignorability, RCTs rely on the Stable Unit Treatment Value Assumption (SUTVA)

"The treatment applied to one unit does not affect the outcome for other units"

11 / 31

SUTVA: No interference

  • Aside from ignorability, RCTs rely on the Stable Unit Treatment Value Assumption (SUTVA)

"The treatment applied to one unit does not affect the outcome for other units"

  • No spillovers

  • No general equilibrium effects

11 / 31

Network effects (spillover) example

  • RCT where students where randomized into two groups:

    • Treatment: Parents receive a text message when student misses school.
    • Control: Parents receive a general text message.
12 / 31

Network effects (spillover) example

  • RCT where students where randomized into two groups:

    • Treatment: Parents receive a text message when student misses school.
    • Control: Parents receive a general text message.

  • Estimate the effect of the intervention on attendance.

    • Difference in average attendance between treated students and control students.
12 / 31

Network effects (spillover) example

  • RCT where students where randomized into two groups:

    • Treatment: Parents receive a text message when student misses school.
    • Control: Parents receive a general text message.

  • Estimate the effect of the intervention on attendance.

    • Difference in average attendance between treated students and control students.

  • Potential problem: Students usually skip school with a friend.

12 / 31

Network effects (spillover) example

  • RCT where students where randomized into two groups:

    • Treatment: Parents receive a text message when student misses school.
    • Control: Parents receive a general text message.

  • Estimate the effect of the intervention on attendance.

    • Difference in average attendance between treated students and control students.

  • Potential problem: Students usually skip school with a friend.

Why could this be a problem for causal inference?

12 / 31

Network effects


Can we do something about this?

13 / 31

Network effects


Can we do something about this?

  1. Randomize at a higher level (e.g. neighborhood, school, etc. instead of at the individual level)
13 / 31

Network effects


Can we do something about this?

  1. Randomize at a higher level (e.g. neighborhood, school, etc. instead of at the individual level)

  2. Model the network!

13 / 31

General Equilibrium Effects

  • Usually arise when you scale up a program or intervention.

  • Imagine you want to test the effect of providing information about employment and expected income to students to see whether it affect their choice of university and/or major.

14 / 31

General Equilibrium Effects

  • Usually arise when you scale up a program or intervention.

  • Imagine you want to test the effect of providing information about employment and expected income to students to see whether it affect their choice of university and/or major.

    What could happen if you offer it to everyone?

14 / 31

Let's see another example

15 / 31

Get Out The Vote

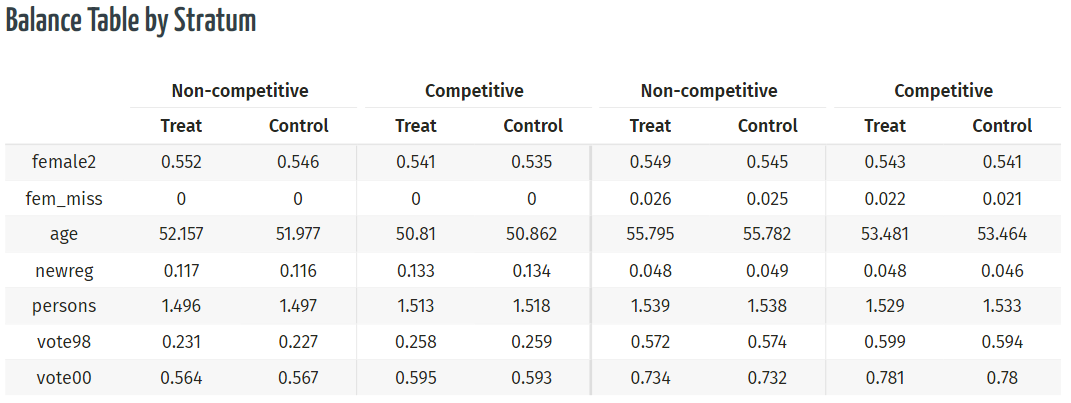
  • "Get out the Vote" Large-Scale Mobilization experiment (Arceneaux, Gerber, and Green, 2006)

    • "Households containing one or two registered voters where randomly assigned to treatment or control groups"

    • Treatment: GOTV phone calls

    • Stratified RCT: Two states divided into competitive and noncompetitive (randomized within state-competitiveness)

16 / 31

Checking for balance

17 / 31







Let's go to R

18 / 31

Estimating the effect

  • One important thing to note in the previous analysis is that assignment to treatment \(\neq\) contact
d_s1 %>% count(treat_real, contact)
##   treat_real contact     n
## 1          0       0 17186
## 2          1       0  1626
## 3          1       1  1374
19 / 31

Estimating the effect

  • One important thing to note in the previous analysis is that assignment to treatment \(\neq\) contact
d_s1 %>% count(treat_real, contact)
##   treat_real contact     n
## 1          0       0 17186
## 2          1       0  1626
## 3          1       1  1374

Does this break the ignorability assumption?

19 / 31

Estimating the effect

  • One important thing to note in the previous analysis is that assignment to treatment \(\neq\) contact
d_s1 %>% count(treat_real, contact)
##   treat_real contact     n
## 1          0       0 17186
## 2          1       0  1626
## 3          1       1  1374

Does this break the ignorability assumption?

  • Non-compliance: When the treatment assignment (e.g. calling the household) is not the same as the treatment (e.g. actually receiving a call/ making contact with the household)

  • What was randomly assigned was calling the household.

  • Usually, the effect of calling should be lower than the effect of actually receiving the call.

19 / 31






Can we do something if we can't randomize??

20 / 31

Controlling by Confounders

21 / 31

Controlling by Confounders

  • We can control by a confounder by including it in our regression:

    • After we control for it, we are doing a fair comparison (e.g. "holding X constant")

    Conditional Independence Assumption (CIA)

22 / 31

Controlling by Confounders

  • We can control by a confounder by including it in our regression:

    • After we control for it, we are doing a fair comparison (e.g. "holding X constant")

    Conditional Independence Assumption (CIA)

  • "Conditional on X, the ignorability assumption holds."

22 / 31

Controlling by Confounders

  • We can control by a confounder by including it in our regression:

    • After we control for it, we are doing a fair comparison (e.g. "holding X constant")

    Conditional Independence Assumption (CIA)

  • "Conditional on X, the ignorability assumption holds."

  • But is there another way to control for confounders?

22 / 31

Controlling by Confounders

  • We can control by a confounder by including it in our regression:

    • After we control for it, we are doing a fair comparison (e.g. "holding X constant")

    Conditional Independence Assumption (CIA)

  • "Conditional on X, the ignorability assumption holds."

  • But is there another way to control for confounders?

Matching

22 / 31

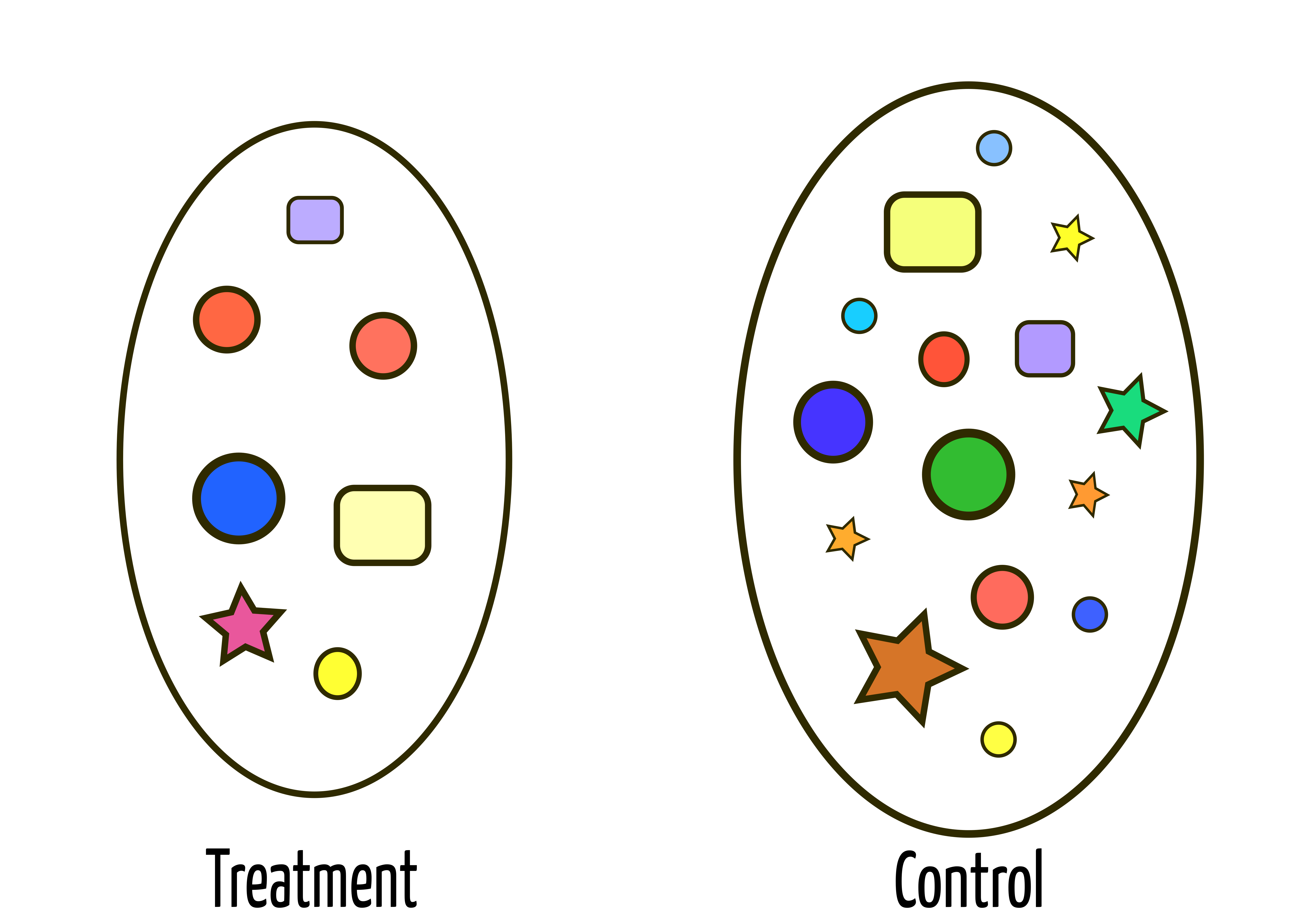
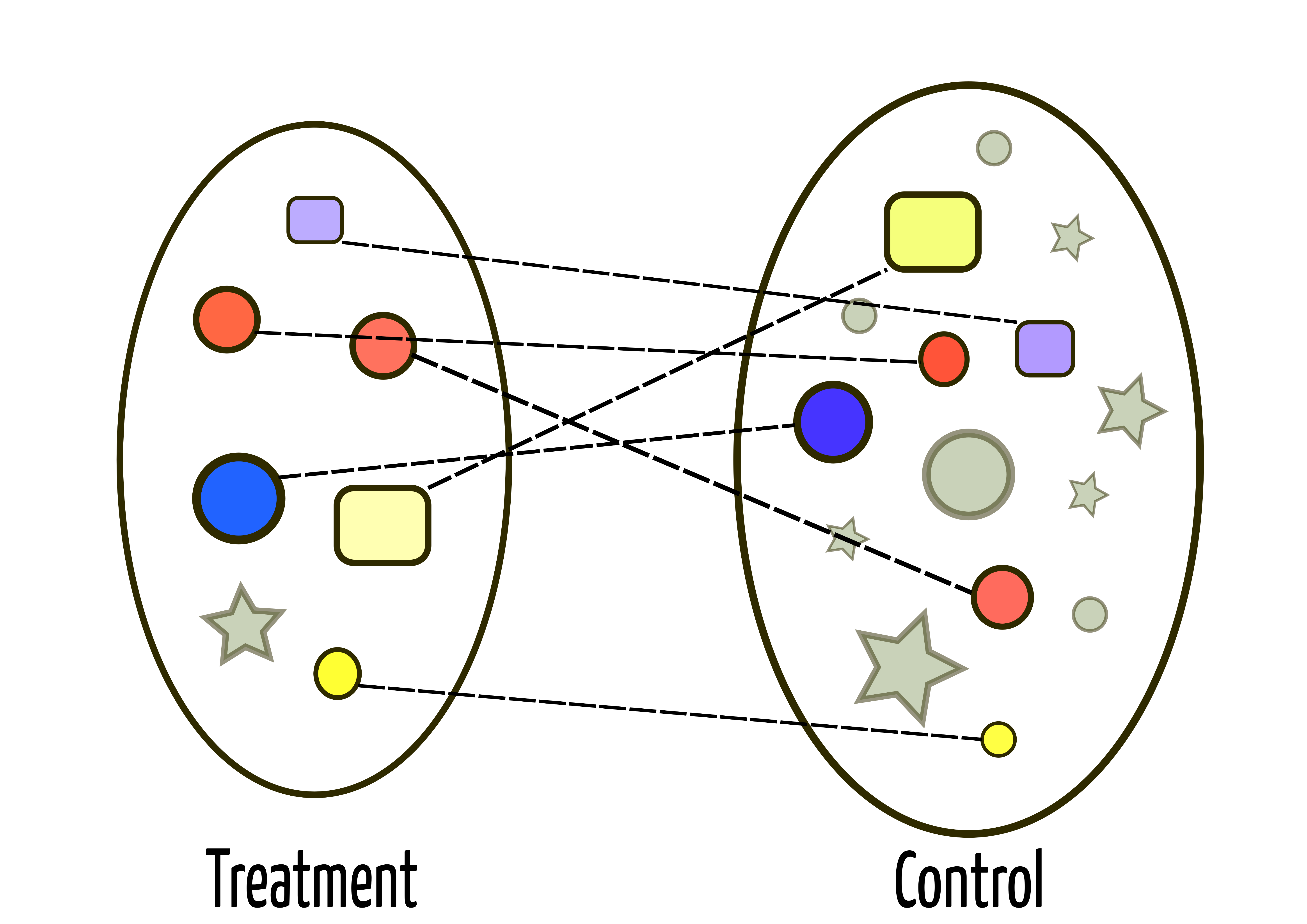
Matching

Start with two groups: A treatment and a control group

23 / 31

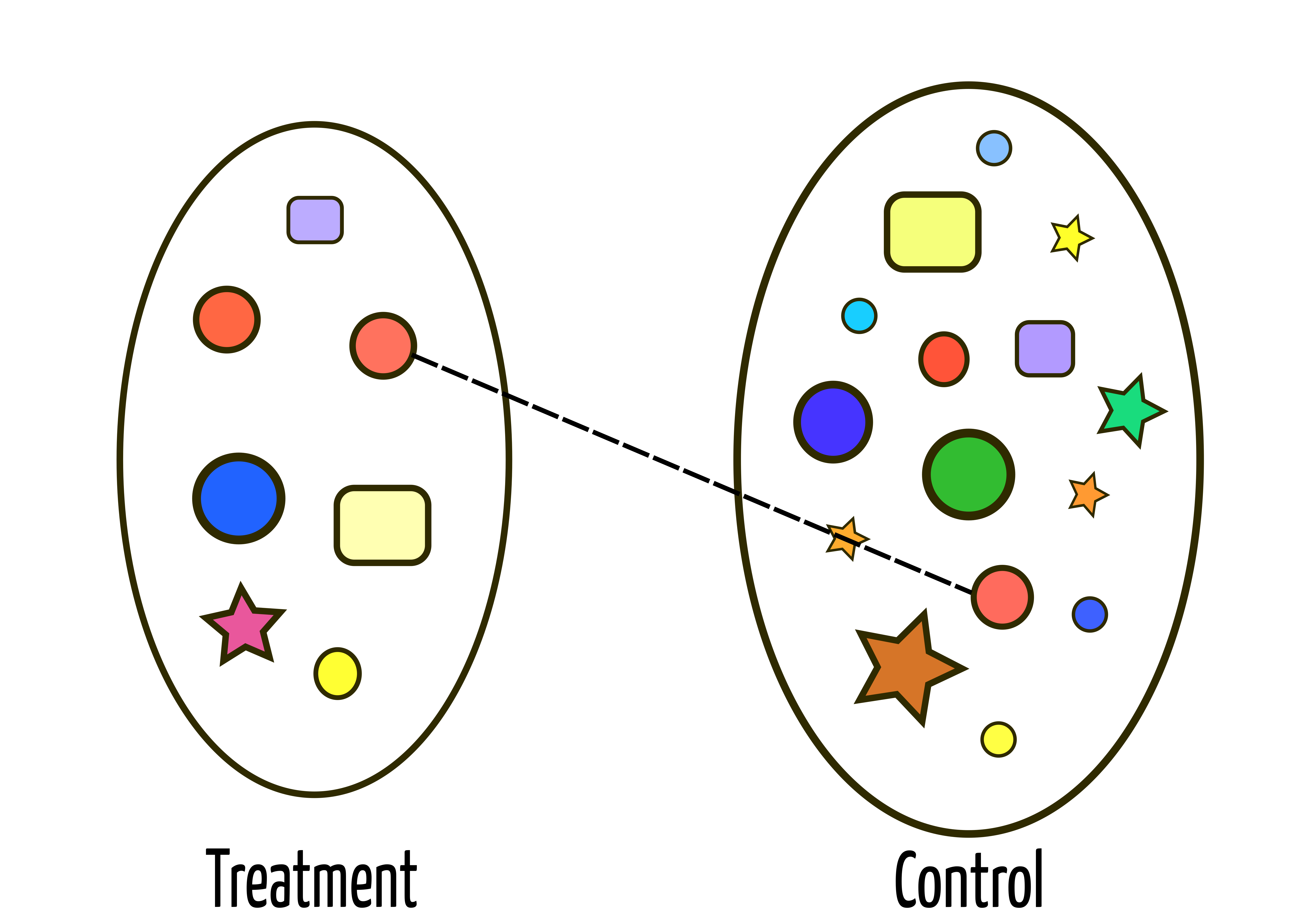
Matching

For each unit in the treatment group, let's find a similar unit in the control group

24 / 31

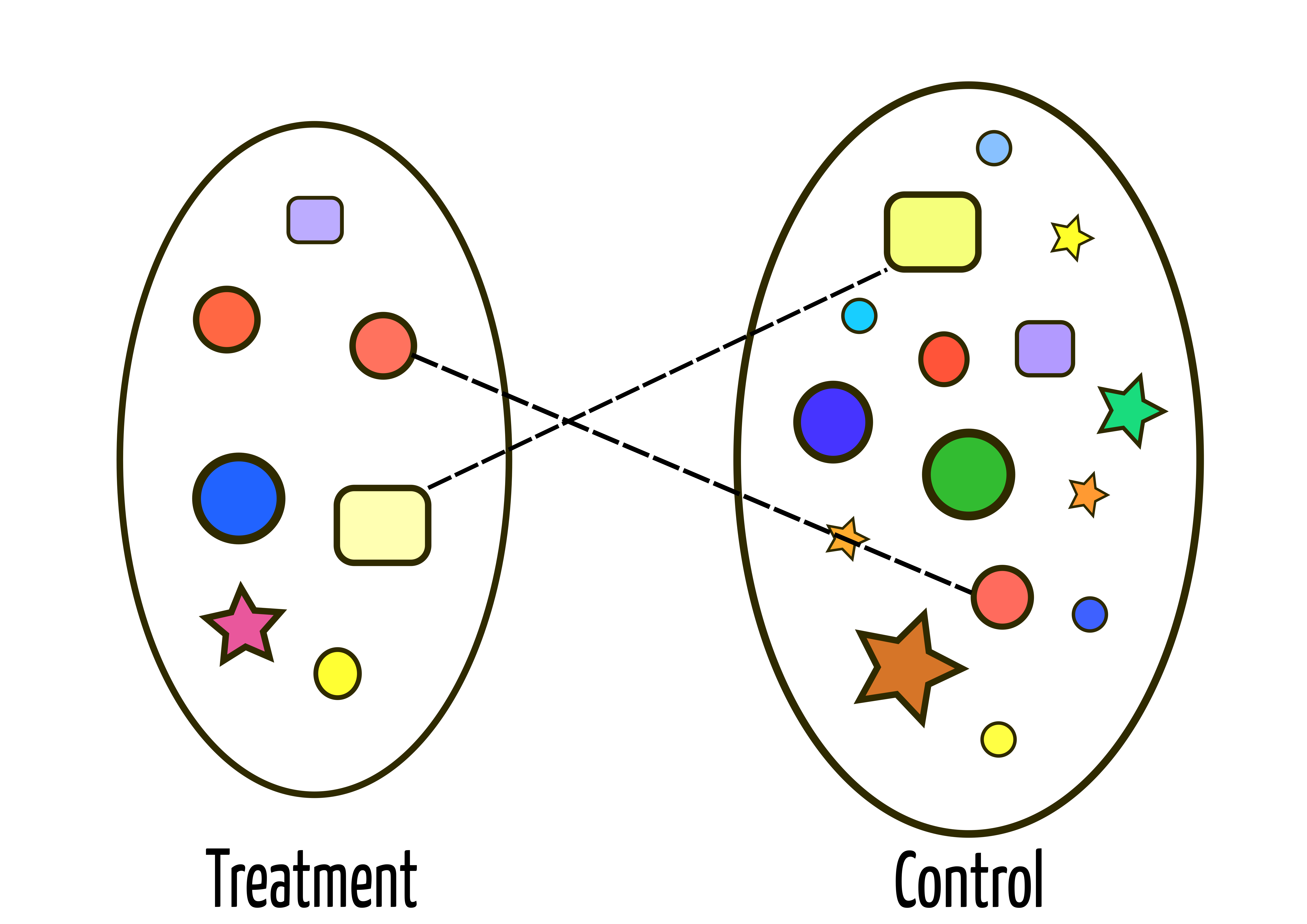
Matching

And we do this for all units

25 / 31

Matching

Note that we might not be able to find similar units for everyone!

26 / 31

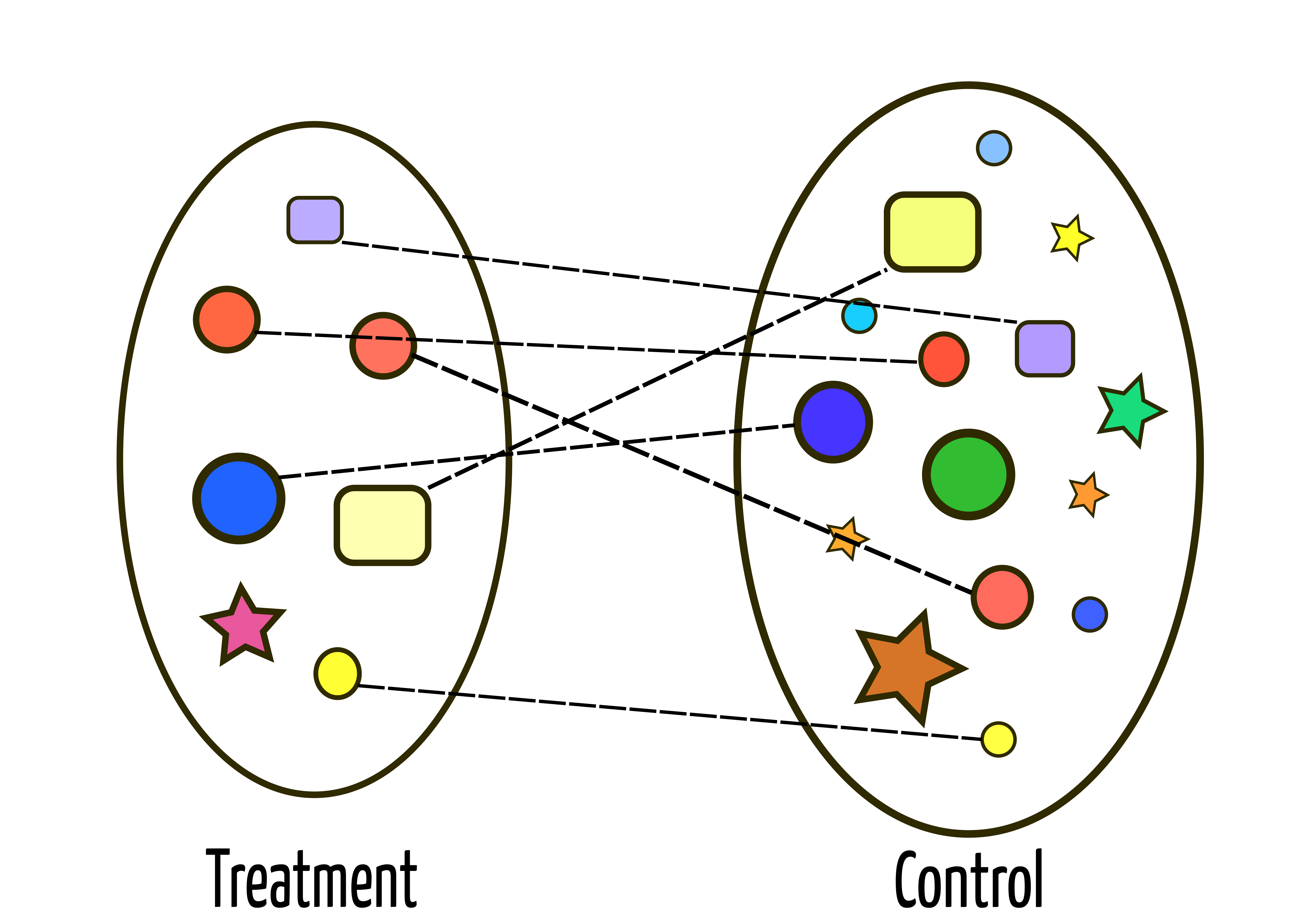
Matching

Then we just compare our matched groups

27 / 31

Propensity Score Matching

  • It is difficult (impossible) to match on all the variables we want (potential confounders)

    • The curse of dimensionality
28 / 31

Propensity Score Matching

  • It is difficult (impossible) to match on all the variables we want (potential confounders)

    • The curse of dimensionality

  • Propensity score: Probability of being in the treatment group given the individuals characteristics.

$$p = Pr(Z = 1) = \hat{\beta}_0 + \hat{\beta}_1X_1 + \hat{\beta}_2X_2 + ... + \hat{\beta}_kX_k$$

  • E.g. Two units have a 50% chance of being treated, but one was actually treated (Z=1) and the other one was not (Z=0).
28 / 31

Propensity Score Matching

  • It is difficult (impossible) to match on all the variables we want (potential confounders)

    • The curse of dimensionality

  • Propensity score: Probability of being in the treatment group given the individuals characteristics.

$$p = Pr(Z = 1) = \hat{\beta}_0 + \hat{\beta}_1X_1 + \hat{\beta}_2X_2 + ... + \hat{\beta}_kX_k$$

  • E.g. Two units have a 50% chance of being treated, but one was actually treated (Z=1) and the other one was not (Z=0).

  • Don't need to calculate this by hand; we will use the MatchIt package.

28 / 31







Let's go to R

29 / 31

Omitted Variable Bias

  • If we are under the presence of confounders, then our estimates will be biased (i.e. will not recover the true causal effect) unless we are able to control by them.
30 / 31

Omitted Variable Bias

  • If we are under the presence of confounders, then our estimates will be biased (i.e. will not recover the true causal effect) unless we are able to control by them.

  • Omitted Variable Bias represents the bias that stems from not being able to observe a confounding variable.

30 / 31

Omitted Variable Bias

  • If we are under the presence of confounders, then our estimates will be biased (i.e. will not recover the true causal effect) unless we are able to control by them.

  • Omitted Variable Bias represents the bias that stems from not being able to observe a confounding variable.

  • If a potential confounder is in our data, then it's not a problem!

    • We can control for it.
30 / 31

Omitted Variable Bias

  • If we are under the presence of confounders, then our estimates will be biased (i.e. will not recover the true causal effect) unless we are able to control by them.

  • Omitted Variable Bias represents the bias that stems from not being able to observe a confounding variable.

  • If a potential confounder is in our data, then it's not a problem!

    • We can control for it.

  • Our headache will come from unobserved confounders.

30 / 31

Wrapping things up

  • If the ignorability assumption doesn't hold, I can potentially control by all my confounders.

    • Conditional Independence Assumption.

  • Unlikely to hold

  • Do we have other alternatives?

    • Let's see next class!

31 / 31

Housekeeping

  • Let's talk about ChatGPT.

    • Should be use as a complement of learning, not a substitute.

    • ChatGPT is mainly useful when you are able to check the accuracy of its answers.

    • You need to do your own work.

2 / 31
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow