Housekeeping

• Homework 2 is due this Friday.

  • Remember to ask questions in advance! (Discussion board for general q's/clarifications; email/OH if it shows your work)
  • Check your full code before submission: Instructions on the course website.

• About JITT feedback:

  • Thanks for questions/suggestions!
  • Currently ~90% ok with pace.
  • Additional support is available.

• No OH next Thursday (09/28) (changed to Tuesday; check OH calendar).

Last week

Today

Look at your green piece of paper and go to the following website

I will now decide whether you go to the hospital or not!

Potential Outcomes

• Last week we discussed potential outcomes, (e.g. $Y_i\left(1\right)$ and $Y_i\left(0\right)$):

  "The outcome that we would have observed under different scenarios"

• Potential outcomes are related to your choices/possible conditions:

  • One for each path!
  • Do not confuse them with the values that your outcome variable can take.

• Definition of Individual Causal Effect:

$$IC{E}_i=Y_i\left(1\right)-Y_i\left(0\right)$$

What was the problem with comparing the sample means to get a causal effect?

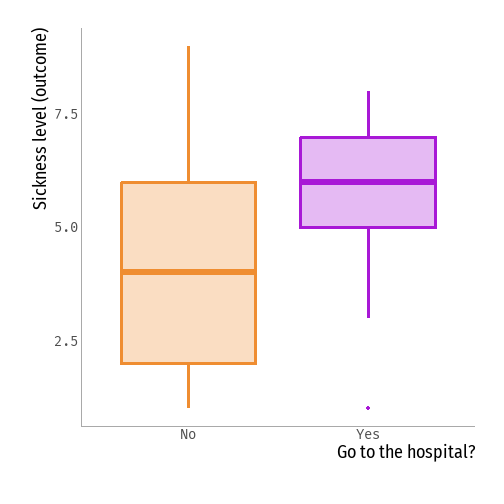
Remember our exercise last week!

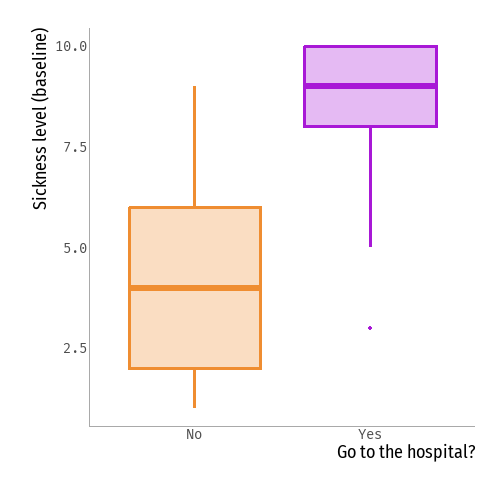
Under what assumptions is our estimate causal?

We are using a difference in means: $$\hat{\tau }=\frac{1}{n_1}\sum _{i\in Z=1}{Y}_i-\frac{1}{n_0}\sum _{i\in Z=0}{Y}_i)$$ to estimate:

$$\tau =E\left[Y_i\right(1)-Y_i(0\left)\right]$$

Under what assumptions is our estimate causal?

We are using a difference in means: $$\hat{\tau }=\frac{1}{n_1}\sum _{i\in Z=1}{Y}_i-\frac{1}{n_0}\sum _{i\in Z=0}{Y}_i)$$

to estimate:

$$\tau =E\left[Y_i\right(1)-Y_i(0\left)\right]$$

Let's do some math

Under what assumptions is our estimate causal?

$$\tau =E\left[Y_i\right(1)-Y_i(0\left)\right]=E\left[Y_i\right(1\left)\right]-E\left[Y_i\right(0\left)\right]$$

• Can we observe $E\left[Y_i\right(1\left)\right]$? and $E\left[Y_i\right(0\left)\right]$?

Key assumption:

Ignorability

Ignorability means that the potential outcomes $Y\left(0\right)$ and $Y\left(1\right)$ are independent of the treatment, e.g. $\left(Y\right(0),Y(1\left)\right)\perp \perp Z$.

$$E\left[Y_i\right(1)|Z=0]=E\left[Y_i\right(1)|Z=1]=E\left[Y_i\right(1\left)\right]$$ and

$$E\left[Y_i\right(0)|Z=0]=E\left[Y_i\right(0)|Z=1]=E\left[Y_i\right(0\left)\right]$$

Under what assumptions is our estimate causal?

$$\tau =E\left[Y_i\right(1)-Y_i(0\left)\right]=E\left[Y_i\right(1\left)\right]-E\left[Y_i\right(0\left)\right]$$

Key assumption:

Ignorability

Ignorability means that the potential outcomes $Y\left(0\right)$ and $Y\left(1\right)$ are independent of the treatment, e.g. $\left(Y\right(0),Y(1\left)\right)\perp \perp Z$.

$$E\left[Y_i\right(1)|Z=0]=\stackrel{\text{Obs. Outcome for T}}{\stackrel{}{E\left[Y_i\right(1)|Z=1]}}=E\left[Y_i\right(1\left)\right]$$ and

$$\underset{\text{Obs. Outcome for C}}{\underset{}{E\left[Y_i\right(0)|Z=0]}}=E\left[Y_i\right(0)|Z=1]=E\left[Y_i\right(0\left)\right]$$

Under what assumptions is our estimate causal?

$$\tau =E\left[Y_i\right(1)-Y_i(0\left)\right]=E\left[Y_i\right(1\left)\right]-E\left[Y_i\right(0\left)\right]$$

• Under ignorability (see previous slide), $E\left[Y_i\right(1\left)\right]=E\left[Y_i\right(1)|Z=1]=E[Y_i|Z=1]$ and $E\left[Y_i\right(0\left)\right]=E\left[Y_i\right(0)|Z=0]=E[Y_i|Z=0]$, then:

$$\tau =E\left[Y_i\right(1\left)\right]-E\left[Y_i\right(0\left)\right]=\underset{\text{Obs. Outcome for T}}{\underset{}{E\left[Y_i\right(1)|Z=1]}}-\stackrel{\text{Obs. Outcome for C}}{\stackrel{}{E\left[Y_i\right(0)|Z=0]}}=E[Y_i|Z=1]-E[Y_i|Z=0]$$

• If the ignorability assumption holds, we can use the difference in means between two groups to estimate the average treatment effect.

Let's see an example: Why did you enroll in the Honors program?

Let's see the distributions of potential outcomes

Let's see the distributions of potential outcomes

We can only observe one distribution per group!

Under Ignorability Assumption

What about if the ignorability assumption doesn't hold?

What can we do to make the ignorability assumption hold?

The problem with self-selection

The power of randomization

• One way to make sure the ignorability assumption holds is to do it by design:

Randomize the assignment of Z

i.e. Some units will randomly be chosen to be in the treatment group and others to be in the control group.

What does randomization buy us?

The power of randomization

• One way to make sure the ignorability assumption holds is to do it by design:

Randomize the assignment of Z

i.e. Some units will randomly be chosen to be in the treatment group and others to be in the control group.

What does randomization buy us?

No (systematic) selection on observables OR unobservables

Randomization of z

Non-Experimental Causal Graph

• Confounder is a variable that affects both the treatment AND the outcome

Let's identify some confounders

• Estimate the effect of insurance vs no insurance on number of accidents $\to$ Compare people with insurance vs people without insurance.

• Estimate the effect of attending office hours vs not attending on your grade $\to$ Compare people who attend OH vs people who don't.

Experimental Causal Graph

• Due to randomization, we know that the treatment is not affected* by a confounder

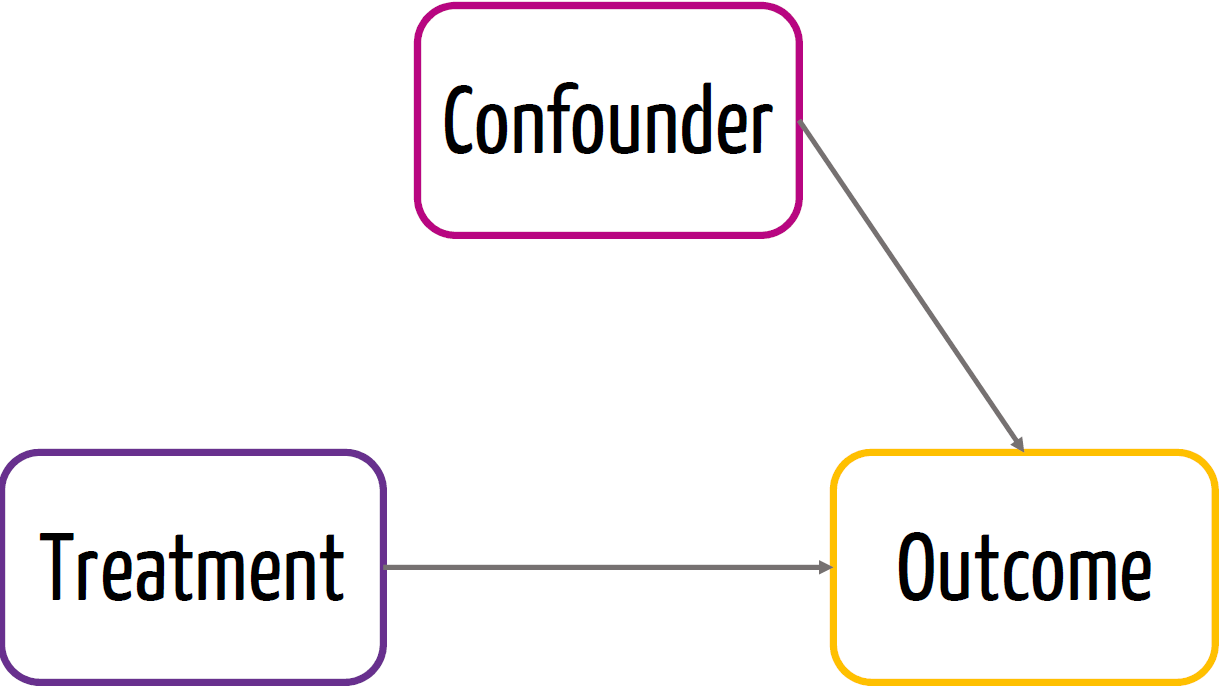
If I randomize treatment allocation...

Just by chance!

RCTs: The Gold Standard

How to analyze RCTs?

How to analyze RCTs?

Easy! (Statistically speaking)

How to analyze RCTs?

Easy! (Statistically speaking)

1) Check for balance

How to analyze RCTs?

Easy! (Statistically speaking)

1) Check for balance
2) Calculate difference in sample means between treatment and control group

Are Emily and Greg More Employable Than Lakisha and Jamal?

• Actual field experiment conducted in Boston and Chicago.

• Send out resumes with randomly assigned names:

  • Female- and male-sounding names.

  • White- and African American-sounding names

• Measure whether applicant was called back

Are Emily and Greg More Employable Than Lakisha and Jamal?

Other potential issues to have in mind

Generalizability of our estimated effects

• Where did we get our sample for our study from? Is it representative of a larger population?

Spillover effects

• Can an individual in the control group be affected by the treatment?

General equilibrium effects

• What happens if we scale up an intervention? Will the effect be the same?

Next class

References

• Angrist, J. and S. Pischke. (2015). "Mastering Metrics". Chapter 1.

• Heiss, A. (2020). "Program Evaluation for Public Policy". Class 7: Randomization and Matching, Course at BYU

• Imbens, G. and D. Rubin. (2015). "Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction". Chapter 1