Announcements

• Homework 5 is due this Friday (remember to get an early start!)

• Next class: No new content, only a review! (Final TRIVIA)

• One final JITT: Only a Knowledge Check (due Sunday before class for Monday section).

  • Make sure you do it this week, so you don't have to work during the break.

What we have seen...

What we'll cover today

Quick refresher on decision trees

To split or not to split

Let's look at an example: Car seat prices

# Data for ISLR
Carseats = read.csv("https://raw.githubusercontent.com/maibennett/sta235/main/exampleSite/content/Classes/Week13/1_RandomForests/data/Carseats.csv")
head(Carseats)

##   Sales CompPrice Income Advertising Population Price ShelveLoc Age Education
## 1  9.50       138     73          11        276   120       Bad  42        17
## 2 11.22       111     48          16        260    83      Good  65        10
## 3 10.06       113     35          10        269    80    Medium  59        12
## 4  7.40       117    100           4        466    97    Medium  55        14
## 5  4.15       141     64           3        340   128       Bad  38        13
## 6 10.81       124    113          13        501    72       Bad  78        16
##   Urban  US
## 1   Yes Yes
## 2   Yes Yes
## 3   Yes Yes
## 4   Yes Yes
## 5   Yes  No
## 6    No Yes

Do you wanna build a... tree?

library(caret)
library(rpart)
library(rattle)
library(rsample)
library(modelr)
set.seed(100)
split = initial_split(Carseats, prop = 0.7, strata = "Sales")
carseats.train = training(split)
carseats.test = testing(split)
tuneGrid = expand.grid(cp = seq(0, 0.015, length = 100))
mcv = train(Sales ~., data = carseats.train, method = "rpart", 
  trControl = trainControl("cv", number = 10), tuneGrid = tuneGrid)

Do you wanna build a... tree?

library(caret)
library(rpart)
library(rattle)
library(rsample)
library(modelr)
set.seed(100)
split = initial_split(Carseats, prop = 0.7, strata = "Sales")
carseats.train  = training(split)
carseats.test   = testing(split)
tuneGrid = expand.grid(cp = seq(0, 0.015, length = 100))
mcv = train(Sales ~., data = carseats.train, method = "rpart", 
  trControl = trainControl("cv", number = 10), tuneGrid = tuneGrid)

Do you wanna build a... tree?

fancyRpartPlot(mcv$finalModel, caption="Decision Tree for Car Seats Sales")

Introduction to Bagging

• Bagging (Bootstrap Aggregation): Meant to reduce variance.

• Remember bootstrap sampling?

Introduction to Bagging

• Bagging (Bootstrap Aggregation): Meant to reduce variance.

• Remember bootstrap sampling?

Introduction to Bagging

• Bagging (Bootstrap Aggregation): Meant to reduce variance.

• Remember bootstrap sampling?

Introduction to Bagging

• Bagging (Bootstrap Aggregation): Meant to reduce variance.

• Remember bootstrap sampling?

Introduction to Bagging

• Bagging (Bootstrap Aggregation): Meant to reduce variance.

• Remember bootstrap sampling?

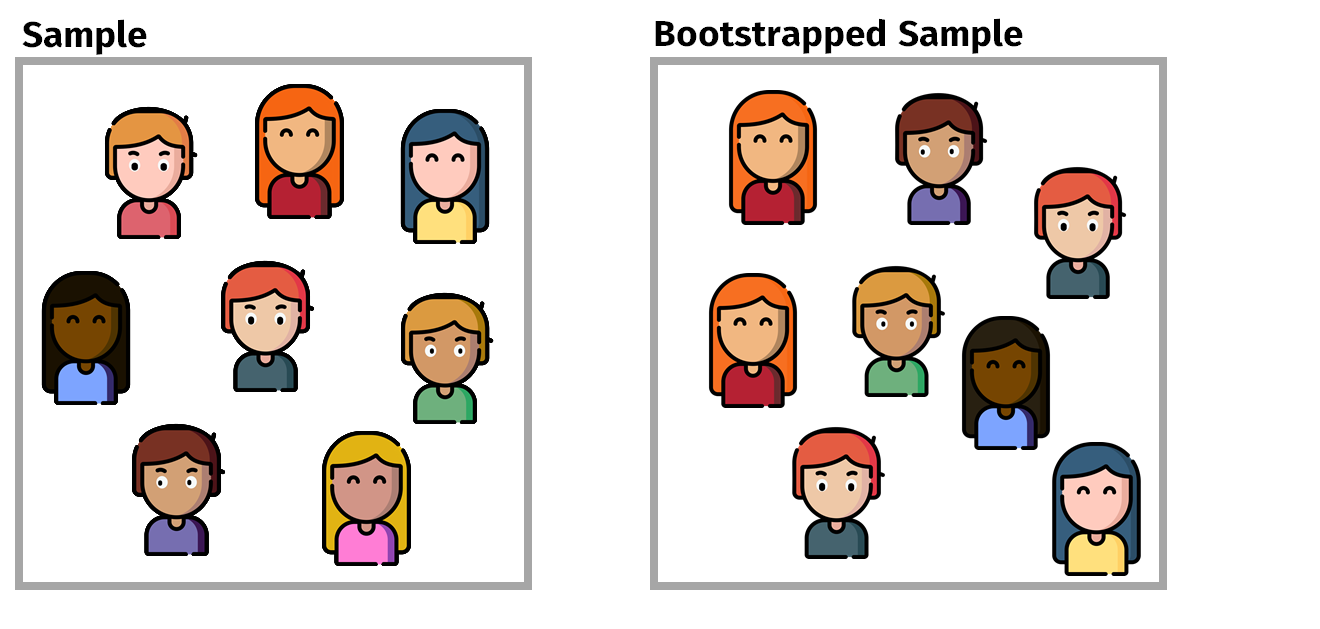
Bagging and Decision Trees

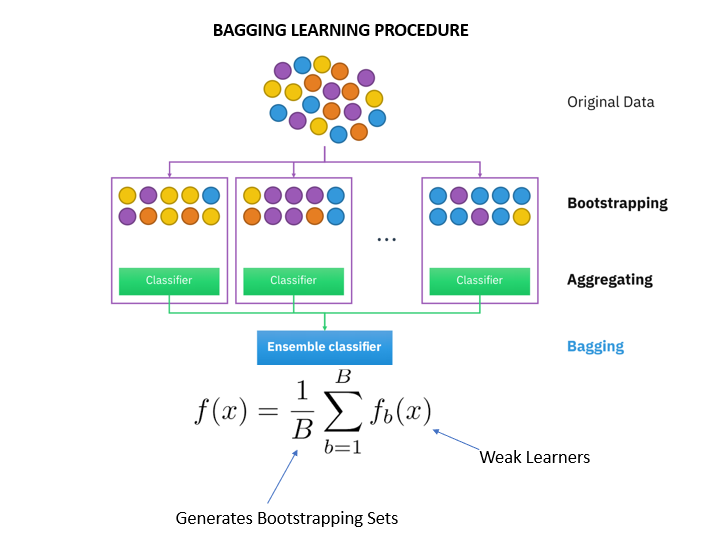
Source: Singhal (2020)

But... how does this reduce variance?

$${\hat{f}}_{bag}\left(x\right)=\frac{1}{B}\sum _{b=1}^B{\hat{f}}^b\left(x\right)$$

• If $Var\left({\hat{f}}^b\right(x\left)\right)={\sigma }^2\forall b$, then:

$$Var\left({\hat{f}}_{bag}\right(x\left)\right)=Var\left(\frac{1}{B}\sum _{b=1}^B{\hat{f}}^b\right(x\left)\right)=\frac{B}{B^2}{\sigma }^2=\frac{{\sigma }^2}{B}$$

How do we do this in R?

set.seed(100)
bt = train(Sales ~ ., data = carseats.train,
            method = "treebag", 
            trControl = trainControl("cv", number = 10),
            nbagg = 100, 
            control = rpart.control(cp = 0))

How do we do this in R?

set.seed(100)
bt = train(Sales ~ ., data = carseats.train,
            method = "treebag",
            trControl = trainControl("cv", number = 10),
            nbagg = 100, 
            control = rpart.control(cp = 0))

How do we do this in R?

set.seed(100)
bt = train(Sales ~ ., data = carseats.train,
            method = "treebag",
            trControl = trainControl("cv", number = 10),
            nbagg = 100,
            control = rpart.control(cp = 0))

How do we do this in R?

set.seed(100)
bt = train(Sales ~ ., data = carseats.train,
            method = "treebag",
            trControl = trainControl("cv", number = 10),
            nbagg = 100, 
            control = rpart.control(cp = 0))

How does it compare to the best single decision tree?


Let's see!

Best DT vs Bagging

• RMSE for single decision tree:

rmse(mcv, carseats.test)

## [1] 2.025994

• RMSE for bagged trees (100):

rmse(bt, carseats.test)

## [1] 1.523912

Best DT vs Bagging

Interpretability?

set.seed(100)
bt = train(Sales ~ ., data = carseats.train, method = "treebag", 
            trControl = trainControl("cv", number = 10),
            nbagg = 100, control = rpart.control(cp = 0))
plot(varImp(bt, scale = TRUE))

Bringing trees together

• Random Forests uses both the concepts of decision trees and bagging, but also de-correlates the trees.

Bootstrap: Vary n dimension (rows/obs)

De-correlation: Vary p dimension (number of predictors)

• For each bagged tree, choose m out of p regressors.

Basic algorithm

1.  Given a training data set
2.  Select number of trees to build (n_trees)
3.  for i = 1 to n_trees do
4.  |  Generate a bootstrap sample of the original data
5.  |  Grow a regression/classification tree to the bootstrapped data
6.  |  for each split do
7.  |  | Select m_try variables at random from all p variables
8.  |  | Pick the best variable/split-point among the m_try
9.  |  | Split the node into two child nodes
10. |  end
11. | Use typical tree model stopping criteria to determine when a 
    | tree is complete (but do not prune)
12. end
13. Output ensemble of trees 

Source: Boehmke & Greenwell (2020)

Back to our example!

set.seed(100)
tuneGrid = expand.grid(
  mtry = 1:11,
  splitrule = "variance",
  min.node.size = 5
)
rfcv = train(Sales ~ ., data = carseats.train,
             method = "ranger", 
             trControl = trainControl("cv", number = 10),
             importance = "permutation",
             tuneGrid = tuneGrid)
plot(rfcv)

Back to our example! (Runs faster: 30s vs 11s)

library(doParallel)
cl = makePSOCKcluster(7)
registerDoParallel(cl)
set.seed(100)
rfcv_fast = train(Sales ~ ., data = carseats.train,
                   method = "ranger", 
                   trControl = trainControl("cv", number = 10, 
                                            allowParallel = TRUE),
                   tuneGrid = tuneGrid)
stopCluster(cl)
registerDoSEQ()

Covariance importance?

plot(varImp(rfcv, scale = TRUE))

Let's compare our models:

# Pruned tree
rmse(mcv, carseats.test)

## [1] 2.025994

# Bagged trees
rmse(bt, carseats.test)

## [1] 1.523912

# Random Forest
rmse(rfcv, carseats.test)

## [1] 1.476309

What is boosting?

• Similar to bagging, but now trees grow sequentially.

• Slowly learning!

• More effective on models with high bias and low variance

Tuning parameters for boosting

• Number of trees: We need to select the $B$ number of trees we will fit. We can get this through cross-validation.

• Shrinkage parameter: $\lambda$ determines how fast the boosting will learn. Typical numbers range are 0.001 to 0.01. If your algorithm is learning too slow (low $\lambda$), you're going to need a lot of trees!

• Number of splits: Number of splits $d$ controls the complexity of your trees. We usually work with low-complexity trees (d=1)

Boosting in R

• There are different types of boosting:

  • Gradient boosting (GBM): Improve on residuals of weak learners

  • Adaptive boosting (AdaBosst): Larger weights for wrong classifications.

modelLookup("ada")

##   model parameter          label forReg forClass probModel
## 1   ada      iter         #Trees  FALSE     TRUE      TRUE
## 2   ada  maxdepth Max Tree Depth  FALSE     TRUE      TRUE
## 3   ada        nu  Learning Rate  FALSE     TRUE      TRUE

modelLookup("gbm")

##   model         parameter                   label forReg forClass probModel
## 1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE      TRUE
## 2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE      TRUE
## 3   gbm         shrinkage               Shrinkage   TRUE     TRUE      TRUE
## 4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE      TRUE

Gradient Boosting in R

set.seed(100)
gbm = train(Sales ~ ., data = carseats.train,
             method = "gbm", 
             trControl = trainControl("cv", number = 10),
             tuneLength = 20)

Gradient Boosting in R

# Final Model information
gbm$finalModel

## A gradient boosted model with gaussian loss function.
## 400 iterations were performed.
## There were 11 predictors of which 11 had non-zero influence.

# Best Tuning parameters?
gbm$bestTune

##   n.trees interaction.depth shrinkage n.minobsinnode
## 8     400                 1       0.1             10

Let's do a comparison!

# Pruned tree
rmse(mcv, carseats.test)

## [1] 2.025994

# Bagged trees
rmse(bt, carseats.test)

## [1] 1.523912

# Random Forest
rmse(rfcv, carseats.test)

## [1] 1.476309

# Gradient Boosting
rmse(gbm, carseats.test)

## [1] 1.212779

Main takeaway points

References

• Boehmke, B. & B. Greenwell. (2020). "Hands-on Machine Learning with R"

• James, G. et al. (2021). "Introduction to Statistical Learning with Applications in R". Springer. Chapter 8.

• Singhal, G. (2020). "Ensemble methods in Machine Learning: Bagging vs. Boosting"